양자역학의 기본개념

[최무영의 과학이야기] <37> 양자역학 ②

원자를 고전역학의 틀로 이해하려 한 러더포드 모형에 문제가 있음을 알게 됐고, 빛과 더불어 물질의 이중성이 관측되었습니다. 이들은 고전역학으로는 해석할 수 없는 현상들입니다. 고전역학의 관점에서는 알갱이와 파동은 완전히 다른 실체와 현상입니다. 따라서 어떤 대상이 알갱이면 알갱이고 파동이면 파동이지, 알갱이기도 하고 파동이기도 하다는 이중성이란 있을 수 없는 것입니다. 그래서 이중성이 관측되었다는 사실은 본질적으로 고전역학의 체계를 바꿔야 한다는 것을 암시하였고, 여기서 나타나게 된 것이 바로 새로운 동역학으로서 양자역학입니다.

양자역학은 고전역학과 완전히 다른 개념과 기본원리에서 출발하며, 이에 따라 완전히 다른 관점을 지닙니다. 기본원리 중 하나는 하이젠베르크(Werner Heisenberg)가 생각해낸 불확정성원리(uncertainty principal)입니다. 임의의 물질알갱이의 위치와 운동량을 동시에 정확히는 알 수 없다는 내용인데 식으로는

로 씁니다.

는 위치 x의 불확정도이고

는 운동량 p의 불확정도로서 그 두 가지 불확정도의 곱은 대략 플랑크상수 h보다 작을 수는 없다는 것입니다. 따라서 어떤 알갱이의 위치를 측정해서 그 불확정도

가 작아지면 운동량의 불확정도

는 커지게 됩니다.

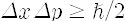
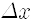
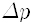
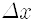
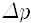
운동량은 불확실해 지는 거지요. 만일 어떤 알갱이의 위치를 완벽하게 정확히 측정했다면 위치의 불확정도가 없으니

이 됩니다. 이 경우에 불확정성원리의 부등식을 만족하려면

가 무한히 커져야 합니다. 이는 그 알갱이의 운동량, 다시 말하면 속도는 전혀 알 수 없게 된다는 것입니다. 또는 반대로 알갱이의 속도를 정확히 재면 그 알갱이의 위치를 모르게 됩니다. 어디 있는지 전혀 알 수가 없다는 말이지요.

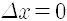
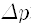
이것은 고전역학의 경우와 완전히 다릅니다. 고전역학에 따르면 주어진 알갱이 또는 물체의 운동 상태는 순간순간마다 그 물체의 위치와 속도로 나타내집니다. 따라서 운동 상태를 말하기 위해서 위치와 속도를 알아내어야 하고 이를 얻어내는 것이 바로 뉴턴의 운동 법칙, 곧 운동방정식이었습니다. 그것이 바로 고전역학의 체계입니다.

그런데 놀랍게도 불확정성원리에 의하면 이건 말이 안 되는 생각입니다. 왜냐하면 애당초 주어진 알갱이의 위치와 속도를 함께 말할 수는 없기 때문입니다. 이는 고전역학의 전제 자체에 완전히 위배되는 것입니다. 고전역학에서는 운동을 기술할 때 위치와 속도를 함께 정확히 측정한다는 것을 전제하고 논의합니다.

불확정성원리는 아주 이상하게 들리겠지만 소리 같은 파동을 생각하면 그리 이상하지 않습니다. 우리가 소리의 위치를 말할 수 있어요? 지금 내가 말할 때 소리가 어디 있어요? 소리가 퍼져나가는 속도는 말할 수 있으나 소리의 위치라는 것은 말할 수 없습니다. 소리는 말하자면 공간에 퍼져있지요. 눈에 보이는 것으로 물결파를 생각해보지요. 잔잔한 호수에 돌을 하나 던져서 물결파가 퍼져나갈 때 퍼져나가는 속도는 말할 수 있지만 물결파가 어디 있는지 위치를 말한다는 것은 별로 의미가 없습니다. 물결파는 전체에 퍼져있는 셈입니다.

이와 비슷하게 전자 같은 물질알갱이도 파동이라고 생각하라는 얘기입니다. 그러면 전자의 속도를 말하면 위치는 말할 수 없게 됩니다. 반면에 전자의 위치를 말하면, 이는 전자를 완전히 알갱이로서 보겠다는 얘기고, 그렇다면 파동의 성격이 없어져서 속도는 말할 수가 없습니다.

전자가 이리로도 가고 저리로도 간다는 말이 이해하기 어렵지요. 그런데 그냥 파동을 보냈다고 합시다. 그러면 파동이 나아가다가 일부는 이리로 가고 일부는 저리로 나가는 것이 이상하지 않지요. 파동으로 생각하면 두 군데 모두 간다고 말하는 것이 사실 당연합니다.

다시 말해서 전자를 고전역학에서 말하는 알갱이라고 생각하면 이리로도 가고 저리로도 간다는 말을 이해할 수 없지만 전자를 그냥 파동이라고 생각해버리면 이상할 것이 없습니다. 빛도 마찬가지입니다. 빛이 파동이라면 한 줄기가 이리로 가고 다른 한 줄기는 저리로 가는 것이 당연하지만 빛을 알갱이, 곧 빛알이라고 생각하면 빛알 하나가 이리로 가고 저리로도 간다는 이상한 문제가 생깁니다.

이러한 사고는 사실 이해하기 어렵습니다. 왜냐하면 우리 모두 일상생활에서 계속 고전역학 체계를 경험하며 자라왔기 때문입니다. 원자나 분자 같은 작은 세계를 직접 감각기관으로 경험하지 못했고, 일상 경험은 항상 고전역학 체계에 길들여져 있으므로 이상하게 보입니다.

예를 들어 만일 플랑크상수가 0이 되었다면 불확정성은 없는 것이며, 이런 경우에는 양자역학이 고전역학과 똑같아집니다. 플랑크상수가 0이 아니기 때문에 양자역학이 고전역학과 다른 것인데, 다행인지 불행인지 플랑크상수는 워낙 작기 때문에 우리 일상 경험에서는 사실상 0이나 마찬가지로 느껴집니다. 그래서 일상에서는 고전역학적인 세계를 경험하는 것입니다.

이러한 불확정성원리를 기본원리로 받아들이면 양자역학에서 운동은 고전역학에서 말하는 운동과 개념상 완전히 달라집니다. 고전역학에서 운동은 위치와 속도에 의해 규정되므로 운동을 기술하려면 순간마다 위치와 속도를 말해야 합니다. 반면에 양자역학에서는 근본적으로 위치와 속도를 말할 수가 없습니다. 따라서 양자역학에서는 운동 개념을 다르게 생각하고, 상태의 규정을 새롭게 해석해야 할 것입니다.

그러면 주어진 알갱이 등 대상의 상태를 어떻게 규정하는가? 양자역학에서는 대상의 상태를 규정하는 상태함수가 존재한다고 전제합니다. 이는 시간 t와 공간에서의 위치 x의 함수인데 보통 그리스 문자 프사이(psi)를 써서

로 표시합니다.

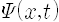
뒤에서 말하겠지만 이 상태함수는 파동을 기술하는 방정식 꼴을 만족하므로 흔히 파동함수(wave function)라고 부르지요. [수학적으로 엄밀하게 말하면 상태는 힐버트 공간(Hilbert space)이라 부르는 추상적인 공간에서 존재하는 벡터로 나타내지는데, 이를 켓(ket)이라 부르며

로 표시합니다. 이러한 추상적인 켓벡터를 위치공간에서 표현한 것이 위에서 말한 상태함수

이지요.]

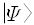
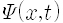
다시 말해서 고전역학에서는 주어진 물체의 위치와 속도를 알면 그 물체의 상태를 아는 것이지만, 양자역학 체계에서는 물체의 상태함수를 알아야 그것의 상태를 아는 것입니다. 상태함수는 일반적으로 위치와 시간의 함수이므로 위치와 시간에 따라 바뀝니다.

(매주 화, 목, 금 연재)